Bloom Filter

• 论文：https://www.tandfonline.com/doi/abs/10.1080/15427951.2004.10129096

• Bloom filter是一种空间效率高的随机数据结构，采用位数组表示一个集合以提供成员查询。Bllom filter是容许错误判断的，即把不属于这个集合的元素误判断属于这一集合，这样的错误称作false positives。因此Bloom filter不适用于零错误的应用，它通过极低的错误率节省了大量的空间。

• The Bloom filter principle: Wherever a list or set is used, and space is at a premium, consider using a Bloom filter if the effect of false positives can be mitigated. (当空间消耗昂贵而允许false positives时，考虑使用布隆过滤器。)

Standard Bloom Filter

• Bllom Filter采用一个$m$位的位数组来表示包含$n$个元素的集合$S=\{x_1,x_2,\dots,x_n\}$，位数组全初始化为$0$。Bllom Filter使用$k$个相互独立的哈希函数，将集合中的每个元素映射到$\{1,\dots,m\}$的范围中。对于集合中的每一个元素$x\in S$，第$i$个$（1\leq i \leq k）$哈希函数映射的位$h_i(x)$被设置为$1$（不进行重复设置）。

• 在判断$y$是否属于集合$S$时，如果所有$h_i(y)$$（1\leq i \leq k）$的位都已经设置为$1$，那么认为$y\in S$，否则$y \notin S$，因此存在将$y$误判为$S$中元素的情况。

  

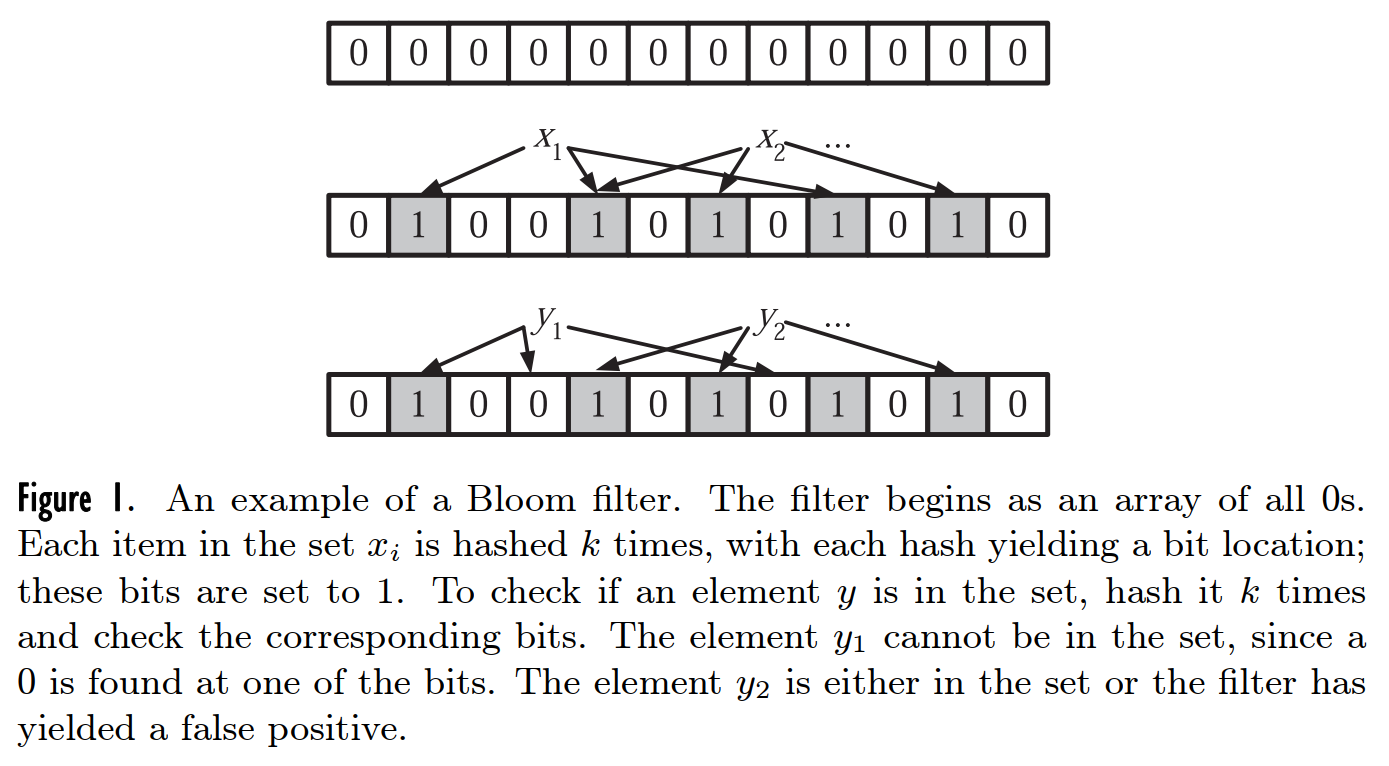
• Bllom Filter在判断一个元素是否属于它表示的集合时会有一定的错误率（false positive rate）。在很多应用中，只要false positive足够小，则可以接受这样的错误。假设$kn<m$且各个哈希函数是完全随机的，则当$S$中的所有元素被哈希映射到Bloom filter后，某一特定位仍然为$0$的概率为

  $$p^{\prime}=\left(1-\frac{1}{m}\right)^{k n} \approx \mathrm{e}^{-k n / m}.$$

  其中$1/m$表示任意一个哈希函数选中这一位的概率（前提是哈希函数是完全随机的），则$(1-1/m)$表示哈希一次没有选中这一位的概率。要把$S$完全映射到位数组中，需要做$kn$次哈希。令$p=e^{-kn/m}$，则$p$近似$p’$(在$O(1/m)$内)。

  令$\rho$为位数组中$0$的比例，则$\mathbb{E}(\rho)=p’$。则错误率（false positive rate）为

  $$(1-\rho)^{k} \approx\left(1-p^{\prime}\right)^{k} \approx(1-p)^{k} .$$

  得到

  $$f^{\prime}=\left(1-\left(1-\frac{1}{m}\right)^{k n}\right)^{k}=\left(1-p^{\prime}\right)^{k}, \\ f=\left(1-\mathrm{e}^{-k n / m}\right)^{k}=(1-p)^{k}.$$

  相比$p’$和$f’$，$p$和$f$更常见于分析中。

• Bllom Filter有另外一种表示方式，则将$m$位位数组平均分给$k$个hash函数，这样每个哈希函数的范围变为$m/k$位。在这种情况下，某一特定位为0的概率为

  $$\left(1-\frac{k}{m}\right)^{n} \approx \mathrm{e}^{-k n / m}.$$

  近似上看，两者的表现类似。但在$k\geq1$时，

  $$\left(1-\frac{k}{m}\right)^{n} \leq\left(1-\frac{1}{m}\right)^{k n}$$

  则精确得到第二种表示方式的false positive rate小于或等于第一种，并且将位按哈希函数划分能够实现并行化。

• 对于给定的$m$与$n$，根据Bllom Filter的原理可以知道：使用更多的哈希函数，那么在对一个不属于集合的元素进行查询时得到$0$的概率就大；而减少哈希函数的个数，则会提高位数组中$0$的比重，因此需要找到最合适的哈希函数值。如上得到$f=\exp \left(k \ln \left(1-\mathrm{e}^{-k n / m}\right)\right)$，设$g=k\ ln(1-e^{-kn/m})$，则寻找$f$的最小值等价于寻找$g$的最小值。求导可得

  $$\frac{\partial g}{\partial k}=\ln \left(1-\mathrm{e}^{-\frac{k n}{m}}\right)+\frac{k n}{m} \frac{\mathrm{e}^{-\frac{k n}{m}}}{1-\mathrm{e}^{-\frac{k n}{m}}}$$

  解得零点$k=ln\ 2\ \cdot\ (m/n)$，该点也是一个全局最优值，对应解得$p=1/2$。在这种情况下，最小错误率$f=(1/2)^k\approx (0.6185)^{m/n}$。同样对于$f’$与$p’$，可以得到当$p’=1/2$时，$g’$取最小值。

A Lower Bound

• 在不超过一定错误率的情况下，Bloom Filter需要设置足够大的$m$才能表示全集中任意$n$个元素的集合。假设全集中共有$u$个元素，允许的最大错误率为$\epsilon$，假设$X$为全集中任取$n$个元素的集合，$F(X)$是表示$X$的位数组。那么对于集合$X$中任意一个元素$x$，在$s = F(X)$中查询$x$都能得到肯定的结果，即$S$能够接受$x$。而Bloom Filter有错误率（false positive rate），对于一个确定的位数组来说，最多接受$n+\epsilon (u-n)$个元素。而一个确定的位数组可以表示$\left(\begin{array}{c}
  n+\epsilon(u-n) \\
  n
  \end{array}\right)$个集合。$m$位的位数组共有$2^m$个不同的组合，全集中共有$\left(\begin{array}{c}
  u \\
  n
  \end{array}\right)$个$n$元素的集合，因此要让$m$位的位数组表示所有$n$个元素的集合，有 $$2^{m}\left(\begin{array}{c} n+\epsilon(u-n) \\ n \end{array}\right) \geq\left(\begin{array}{l} u \\ n \end{array}\right)$$ 即 $$m \geq \log _{2} \frac{\left(\begin{array}{l} u \\ n \end{array}\right)}{\left(\begin{array}{c} n+\epsilon(u-n) \\ n \end{array}\right)} \approx \log _{2} \frac{\left(\begin{array}{l} u \\ n \end{array}\right)}{\left(\begin{array}{c} \epsilon u \\ n \end{array}\right)} \geq \log _{2} \epsilon^{-n}=n \log _{2}(1 / \epsilon)$$ 因此，$m$至少要大于$n \log _{2}(1 / \epsilon)$才能使错误率不大于给定的$\epsilon$。根据上节中$f=(1/2)^k=(1/2)^{ln\ 2\ \cdot\ (m/n)}$，令$f\leq \epsilon$得到 $$m \geq n \frac{\log _{2}(1 / \epsilon)}{\ln 2}=n \log _{2} \mathrm{e} \cdot \log _{2}(1 / \epsilon).$$ 这个结果是我们上面得到的最小值的$log_2e\approx1.44$倍，这说明在哈希函数的个数取到最优时，要让错误率不超过$\epsilon$，$m$至少需要取到最小值的$1.44$倍。

Hashing vs. Bloom Filters

• 哈希函数是常用的用以表示集合的方式，集合的每个元素都被映射到$\Theta(\text{log}\ n)$位上，然后再用一个哈希值的列表（已排序）表示集合。这种方法产生的错误率很小，如果集合中的每个元素用$2\ \text{log}_2\ n$位来表示，则两个特定的元素映射到相同哈希值的可能性为$1/n^2$，而不在集合中的元素与集合中的元素映射到相同哈希值的概率为$n/n^2=1/n$。
• Bloom Filters可以看作哈希的自然推广，它在错误率与采用的位数（空间消耗）中寻找均衡，只有一个哈希函数的Bloom Filters等价于普通的Hashing。Bloom filters产生一个恒定的false positive rate，当用以表示每个集合元素的比特数是恒定的。例如，当$m = 8n$时，false positive rate仅大于0.02。如果需要逐渐消失的错误率，每个元素至少需要采用$\Theta(\text{log}\ n)$位来表示，这也是Bloom Filters不受学术界关注的原因。相反，在实际应用中，为了保持每个元素的位数不变，一个常数错误可能是很有价值的。

　Standard Bloom Filter Tricks

• Bloom filter的简单结构使得某些操作非常容易实现。假设有两个Bloom filter表示集合$S_1$和$S_2$，它们具有相同的比特数，并且使用相同的哈希函数。则一个表示$S_1,S_2$的并集的Bloom filter可以通过原有Bloom filter的两个位向量的OR得到。

• Bloom filter可以很容易地将大小减半，允许应用程序动态地缩小Bloom filter。假设Bloom filter的大小为$2$的幂。将Bloom filter的大小减半，可以将前半部分与后半部分做OR操作得到。当散列进行查找时，最高位可能被屏蔽。

• Bloom filter也可以用来近似两个集合之间的交集。假设有两个Bloom filter表示集合$S_1$和$S_2$，它们具有相同的比特数，并且使用相同的哈希函数。直观地说，这两个位向量的内积是它们相似性的度量。如果第$j$位是被两个Bloom filter同时设置的，那么它是被$S_1\cap S_2$中的元素设置，或者它同时被$S1−(S1∩S2)$中的某个元素和$S2−(S1∩S2)$中的另一个元素设置。则第$j$位被同时设置的概率为

  $$\begin{array}{l} \left(1-\left(1-\frac{1}{m}\right)^{k\left|S_{1} \cap S_{2}\right|}\right) \\ +\left(1-\frac{1}{m}\right)^{k\left|S_{1} \cap S_{2}\right|}\left(1-\left(1-\frac{1}{m}\right)^{k\left|S_{1}-\left(S_{1} \cap S_{2}\right)\right|}\right)\left(1-\left(1-\frac{1}{m}\right)^{k\left|S_{2}-\left(S_{1} \cap S_{2}\right)\right|}\right) \end{array}$$

  化简得到两个Bloom filter的期望内积和为

  $$m\left(1-\left(1-\frac{1}{m}\right)^{k\left|S_{1}\right|}-\left(1-\frac{1}{m}\right)^{k\left|S_{2}\right|}+\left(1-\frac{1}{m}\right)^{k\left(\left|S_{1}\right|+\left|S_{2}\right|-\left|S_{1} \cap S_{2}\right|\right)}\right) .$$

  因此，已知$|S_1|,|S_2|, k, m，$以及内积的大小，可以用上式计算$|S_1∩S_2|$。如果没有给出$|S_1|,|S_2|$，它们也可以通过计算$S_1$,$S_2$的Bloom filter中的$0$位数来估计，集合$S$的$0$位数在其期望$m(1 - 1/m)^{k|S|}$附近。设$Z_1,Z_2$分别为$S_1,S_2$Bloom filter中$0$的个数，$Z_{12}$为内积中$0$的个数，则得到

  $$\frac{1}{m}\left(1-\frac{1}{m}\right)^{-k\left|S_{1} \cap S_{2}\right|} \approx \frac{Z_{1}+Z_{2}-Z_{12}}{Z_{1} Z_{2}}$$

　Counting Bloom Filters

• 假设我们有一个随时间变化的集合，会进行元素插入和删除操作。将元素插入Bloom过滤器只需将元素进行哈希$k$次，并将对应位设为$1$。但不能通过逆过程来执行删除操作，如果我们对要删除的元素进行散列，并将其对应的位设为0。在这种情况下，Bloom filter不再正确地反映集合中的所有元素。

• 为了避免这个问题，Fan等人引入了计数布隆过滤器(counting Bloom filter)的思想。在一个counting Bloom filter中，采用一个计数器来代替位。当元素插入时，相应的计数器增加，当元素删除时，相应的计数器被减少。为了避免计数器溢出，可以选择足够大的计数器。Fan等人的分析表明，每个计数器4位就适用于大多数应用了。

• 要确定一个好的计数器大小，可以考虑一个counting Bloom filter表示$n$个元素的集合，使用$k$个哈希函数和$m$个计数器。设$c(i)$为第$i$个计数器的计数。第$i$个计数器为$j$次的概率是一个二项式随机变量

  $$\mathbb{P}(c(i)=j)=\left(\begin{array}{c} n k \\ j \end{array}\right)\left(\frac{1}{m}\right)^{j}\left(1-\frac{1}{m}\right)^{n k-j} .$$

  任何计数器至少为$j$的概率大于$m\mathbb{P}(c(i)\geq j)$，则

  $$\mathbb{P}(c(i) \geq j) \leq\left(\begin{array}{c} n k \\ j \end{array}\right) \frac{1}{m^{j}} \leq\left(\frac{\mathrm{e} n k}{j m}\right)^{j}$$

  假设$k≤(ln 2)m/n$，因为$k = (ln 2)m/n$获得最佳的false positive rate，则

  $$\mathbb{P}\left(\max _{i} c(i) \geq j\right) \leq m\left(\frac{\mathrm{e} \ln 2}{j}\right)^{j}$$

  如果每个计数器设置为4位，则某个计数器达到16时，计数器就会溢出。从上面公式得到

  $$\mathbb{P}\left(\max _{i} c(i) \geq 16\right) \leq 1.37\times10^{-15}\times m$$

  这个限制适用于最多$n$个项目的集合，这将满足大多数应用程序。另一种解释这个结果的方法是，当有$m\ \text{ln}\ 2$个总计数器增量分布在$m$个计数器上时，计数器的最大值很有可能是$O(\text{log}\ m)$，因此每个计数器只需要$O(\text{log}\ \text{log}\ m)$位。

• 在实践中，当计数器溢出时，一种解决方法是保持它的最大值。只有当计数器最终降至0而它本应保持非0时，这才会导致更多的false positive rate。如果删除是随机的，则此事件的预期时间相对较大。